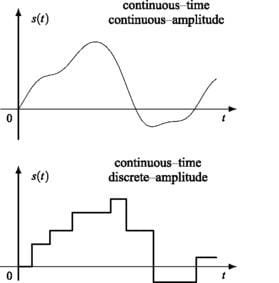
Continuous time Signal
continuous-time signal is a varying quantity (a signal) whose domain, which is often time, is a continuum (e.g., a connected interval of the reals). That is, the function’s domain is an uncountable set. The function itself need not to be continuous.
Properties
- The continuous-time signal is an analog representation of a natural signal.
- Continuous-time variable is denoted by letter t.
- The continuous-time signal can be I converted into discrete-time signal by the Euler’s method.
- The conversion of continuous to discrete time signal is comparatively easy than the conversion of discrete to continuous-time signals.
- The value of the signal can be obtained at any arbitrary point of time.
- It is defined over a finite or infinite domain of sequence.
- The continuous-time signals are not used for the processing of digital signals.
![f(t)=\sin(t),\quad t\in [-\pi ,\pi ]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f5a62642ad4f66510bdde0918bab7caf79c64e6)
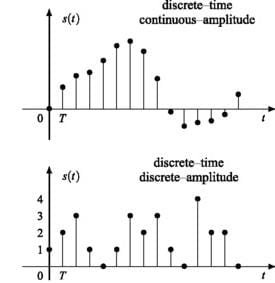
Discrete time Signal
Discrete-time signal is a time series consisting of a sequence of quantities.
Properties
- The discrete-time signal is a digital representation of a continuous-time signal.
- Discrete-time variable is denoted by a letter n.
- Represented by x[n] = [1,2,3,4,5]
- The discrete -time signal can be converted into continuous-time signal by the methods of zero-order hold or first-order hold.
- The conversion of discrete to continuous time signals is very complicated and it is done through a sample and hold process.
- It is defined over a finite domain of sequence.
- The value of the signal can be obtained only at sampling instants of time.
- The discrete-time signals are used for the processing of digital signals.
The District Time Signal is represented by
x[n] = {1,0,1,2,2,1}
↑
The upper arrow is used to show that the value of n is zero(0) at this point.
