Operation on continuous Time Signals | Addition, Multiplication
Operations of CT Signals
-
Amplitude Scaling y(t) = Bx(t)
-
Addition y(t) = x1(t) + x2(t)
-
Multiplication y(t) = x1(t)x2(t)
-
Time Scaling y(t) = x(at)
-
Time Reversal y(t) = x(-t)
-
Time Shifting y(t) = x(t-td)
There are two variable parameters in general:
- Amplitude
- Time
Addition of Signals:
- Point-by-point addition of multiple signals
- Move from left to right (or vice versa), and add
the value of each signal together to achieve the
final signal - y(t) = x (t) + x (t)
- Addition of two signals is nothing but addition of their corresponding amplitudes. This can be best explained by using the following example:

This Picture is taken from YouTube lecture of “Neso Academy”
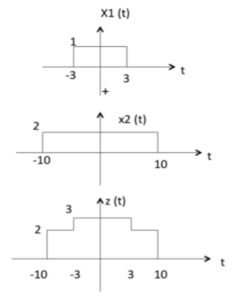
As seen from the diagram above,
- -10 < t < -3 amplitude of z(t) = x1(t) + x2(t) = 0 + 2 = 2
- -3 < t < 3 amplitude of z(t) = x1(t) + x2(t) = 1 + 2 = 3
- 3 < t < 10 amplitude of z(t) = x1(t) + x2(t) = 0 + 2 = 2
Sketch y(t) = u(t) – u(t – 2)

First, plot each of the portions of this signal separately
- x1(t) = u(t) -> Simply a step signal
- x2(t) = –u(t-2) -> Delayed step signal, multiplied by -1
Then, move from one side to the other, and add their instantaneous values
Multiplication of signal
- Point-by-point multiplication of the values
of each signal - y(t) = x1(t)x2(t)
-
Multiplication of two signals is nothing but multiplication of their corresponding amplitudes. This can be best explained by the following example:

This Picture is taken from YouTube lecture of “Neso Academy”
Sketch y(t) = u(t)·u(t – 2)
First, plot each of the portions of this signal separately
- x1(t) = u(t) -> Simply a step signal
- x2(t) = u(t-2) -> Delayed step signal
Then, move from one side to the other, and multiply instantaneous values

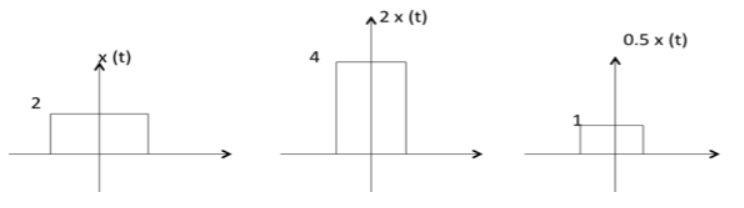
Amplitude Scaling
- Multiply the entire signal by a constant value
- y(t) = Bx(t) [B is a constant]
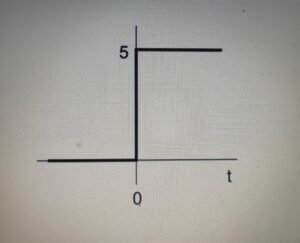
Sketch y(t) = 5u(t)
C x(t) is a amplitude scaled version of x(t) whose amplitude is scaled by a factor C










Hi there friends, its fantastic post about cultureand completely
explained, keep it up all the time.